Week 7
Area
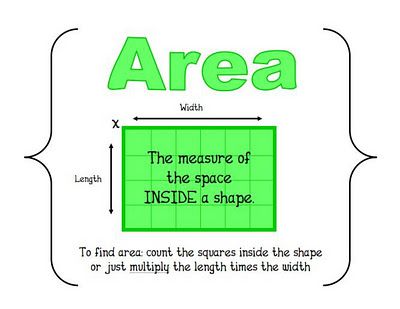
Area is a measure of how much space there is on a flat surface. For example two sheets of paper have twice the area of a single sheet, because there is twice as much space to write on.
Different shapes have different ways to find the area. For example, in a rectangle we find the area by multiplying the length times the width. In the rectangle on the right, the area is 2×4 or 8. If you count the small squares you will find there are 8 of them.
Perimeter
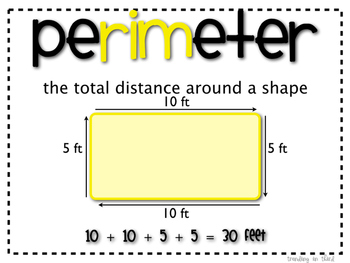
The perimeter is the length of the outline of a shape. To find the perimeter of a rectangle or square you have to add the lengths of all the four sides. x is in this case the length of the rectangle while y is the width of the rectangle.
Circumference
The circumference of a circle is the distance around the outside of the circle. It is like the perimeter of other shapes like squares, but for shapes made up of straight lines, we use the word perimeter and for circles we use the word circumference.
This diagram shows the circumference of a circle.

There are also some other important distances on a circle, called the radius (r) and diameter (d) We will need these to calculate the circumference. The diameter is the distance from one side of the circle, to the other, passing through the center (middle of the circle). The radius is half of this distance.
This diagram shows the circumference, diameter, center and radius on a circle.

How can you calculate the circumference of a circle?
If you know the diameter or radius of a circle, you can work out the circumference. To begin with, remember that pi is a number, written down with the symbol π. π is roughly equal to 3.14. Then, the formula for working out the circumference of the circle is:
Circumference of circle = π x Diameter of circle
which we usually write in the shortened form C = πd. This tells us that the circumference of the circle is three “and a bit” times as long as the diameter. We can see this on the graphic below:
What is Pi?
Circumference & Area
Kaplan p